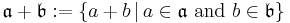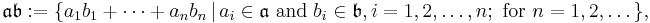Ideal (ring theory)

In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3".

For instance, in rings one studies prime ideals instead of prime numbers, one defines coprime ideals as a generalization of coprime numbers, and one can prove a generalized Chinese remainder theorem about ideals. In a certain class of rings important in number theory, the Dedekind domains, one can even recover a version of the fundamental theorem of arithmetic: in these rings, every nonzero ideal can be uniquely written as a product of prime ideals.

An ideal can be used to construct a quotient ring in a similar way as a normal subgroup in group theory can be used to construct a quotient group. The concept of an order ideal in order theory is derived from the notion of ideal in ring theory.

A fractional ideal is a generalization of an ideal, and the usual ideals are sometimes called integral ideals for clarity.

1 History
2 Definitions
3 Motivation
4 Examples
5 Ideal generated by a set
- 5.1 Example
6 Types of ideals
7 Properties
8 Ideal operations
9 Ideals and congruence relations
10 See also
11 References

History

Ideals were first proposed by Dedekind in 1876 in the third edition of his book Vorlesungen über Zahlentheorie (English: Lectures on Number Theory). They were a generalization of the concept of ideal numbers developed by Ernst Kummer. Later the concept was expanded by David Hilbert and especially Emmy Noether.

Definitions

For an arbitrary ring (R, +, ·), let (R, +) be the underlying additive group. A subset I is called a two-sided ideal (or simply an ideal) of R if

(I, +) is a subgroup of (R, +)
for all x in I and for all r in R, a·r and r·a are in I.

Equivalently, an ideal of R is a sub-R-bimodule of R.

A subset I of R is called a right ideal of R if^[1]

(I, +) is a subgroup of (R, +)
xr is in I for all x in I and all r in R

Equivalently, a right ideal of R is a right R-submodule of R.

A subset I of R is called a left ideal of R if

(I, +) is a subgroup of (R, +)
rx is in I for all x in I and all r in R

Equivalently, a left ideal of R is a left R-submodule of R.

In all cases, the first condition can be replaced by the following

1.′ I is non-empty and for all x, y in I, x − y is in I.^[2]

The left ideals in R are exactly the right ideals in the opposite ring R^o and vice versa. A two-sided ideal is a left ideal that is also a right ideal, and is often called an ideal except to emphasize that there might exist single-sided ideals. When R is a commutative ring, the definitions of left, right, and two-sided ideal coincide, and the term ideal is used alone.

If p is in R, then pR is a right ideal and Rp is a left ideal of R. These are called, respectively, the principal right and left ideals generated by p. To remember which is which, note that right ideals are stable under right-multiplication (IR ⊆ I) and left ideals are stable under left-multiplication (RI ⊆ I).

The connection between cosets and ideals can be seen by switching the operation from "multiplication" to "addition"

We call I a proper ideal if it is a proper subset of R, that is, I does not equal R. The ideal R is called the unit ideal.^[3]

Motivation

Intuitively, the definition can be motivated as follows: Suppose we have a subset of elements Z of a ring R and that we would like to obtain a ring with the same structure as R, except that the elements of Z should be zero (they are in some sense "negligible").

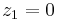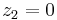But if $z_1=0$ and $z_2=0$ in our new ring, then surely 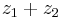$z_1+z_2$ should be zero too, and 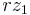$r z_1$ as well as 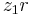$z_1 r$ should be zero for any element $r$ (zero or not).

The definition of an ideal is such that the ideal I generated by Z is exactly the set of elements that are forced to become zero if Z becomes zero, and the quotient ring R/I is the desired ring where Z is zero, and only elements that are forced by Z to be zero are zero. The requirement that R and R/I should have the same structure (except that I becomes zero) is formalized by the condition that the projection from R to R/I is a (surjective) ring homomorphism.

Examples

The even integers form an ideal in the ring Z of all integers; it is usually denoted by 2Z. This is because the sum of any even integers is even, and the product of any integer with an even integer is also even. Similarly, the set of all integers divisible by a fixed integer n is an ideal denoted nZ.
The set of all polynomials with real coefficients which are divisible by the polynomial x² + 1 is an ideal in the ring of all polynomials.
The set of all n-by-n matrices whose last column is zero forms a left ideal in the ring of all n-by-n matrices. It is not a right ideal. The set of all n-by-n matrices whose last row is zero forms a right ideal but not a left ideal.
The ring C(R) of all continuous functions f from R to R contains the ideal of all continuous functions f such that f(1) = 0. Another ideal in C(R) is given by those functions which vanish for large enough arguments, i.e. those continuous functions f for which there exists a number L > 0 such that f(x) = 0 whenever |x| > L.
{0} and R are ideals in every ring R. If R is a division ring or a field, then these are its only ideals.
Compact operators form an ideal in the ring of bounded operators.

Ideal generated by a set

Let R be a ring.

Any intersection of left (resp. right, resp. two-sided) ideals of R is again a left (resp. right, resp. two-sided) ideal of R. Therefore, if X is any subset of R, the intersection of all left (resp. right, resp. two-sided) ideals of R containing X is a left (resp. right, resp. two-sided) ideal I of R, said to be generated by X. I is the smallest left (resp. right, resp. two-sided) ideal of R containing X.

If R is commutative, the left, right and two-sided ideals generated by a subset X of R are the same, since the left, right and two-sided ideals of R are the same. We then speak of the ideal of R generated by X, without further specification. However, if R is not commutative they may not be the same.

The left (resp. right, resp. two-sided) ideal of R generated by a subset X of R is the set of all finite sums of elements of R of the form ra, where r ∈ R and a ∈ X (resp. ar, where r ∈ R and a ∈ X, resp. rar′, where r,r′ ∈ R and a ∈ X). That is, the left (resp. right, resp. two-sided) ideal generated by X is the set of all elements of the form

r₁a₁ + ··· + r_na_n (resp. a₁r₁ + ··· + a_nr_n, resp. r₁a₁r′₁ + ··· + r_na_nr′_n)

with each r_i,r′_i in R and each a_i in X.

By convention, 0 is viewed as the sum of zero such terms, agreeing with the fact that the ideal of R generated by ∅ is {0} by the previous definition.

If a ∈ R, then the left (resp. right, resp. two-sided) ideal of R generated by {a} is denoted by Ra (resp. aR, resp. RaR). Ra is the set of elements of R of the form ra for r ∈ R. An analogous statement holds for aR, but not for RaR.

If an ideal I of R is such that there exists a finite subset X of R (necessarily a subset of I) generating it, then the ideal I is said to be finitely generated.

Example

In the ring Z of integers, every ideal can be generated by a single number (so Z is a principal ideal domain), and the ideal determines the number up to its sign. The concepts of "ideal" and "number" are therefore almost identical in Z. In an arbitrary principal ideal domain this is also true, except that instead of differing only by sign, the various generators of a given ideal may differ multiplicatively by any invertible element of the ring.

Types of ideals

To simplify the description all rings are assumed to be commutative. The non-commutative case is discussed in detail in the respective articles

Ideals are important because they appear as kernels of ring homomorphisms and allow one to define factor rings. Different types of ideals are studied because they can be used to construct different types of factor rings.

Maximal ideal: A proper ideal I is called a maximal ideal if there exists no other proper ideal J with I a subset of J. The factor ring/Quotient ring of a maximal ideal is a field.
Prime ideal: A proper ideal I is called a prime ideal if for any a and b in R, if ab is in I, then at least one of a and b is in I. The factor ring of a prime ideal is an integral domain.
Radical ideal: A proper ideal I is called radical if for any a in R, if aⁿ is in I for some n, then a is in I. The factor ring of a radical ideal is a reduced ring.
Primary ideal: An ideal I is called primary ideal if for all a and b in R, if ab is in I, then at least one of a and bⁿ is in I for some natural number n. Every prime ideal is primary, but not conversely.
Principal ideal: An ideal generated by one element.
Primitive ideal: is the annihilator of a simple left module. A right primitive ideal is defined similarly. Note that (despite the name) left and right primitive ideals are always two-sided ideals. Factor rings constructed with primitive ideals are primitive rings.
Irreducible ideal: An ideal is said to be irreducible if it cannot be written as an intersection of ideals which properly contain it.

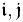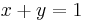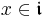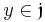Two ideals $\mathfrak{i}, \mathfrak{j}$ are said to be comaximal if $x + y = 1$ for some $x \in \mathfrak{i}$ and $y \in \mathfrak{j}$ .

Properties

An ideal is proper if and only if it does not contain 1.
The proper ideals can be partially ordered via subset inclusion and therefore as a consequence of Zorn's lemma every proper ideal is contained in a maximal ideal.
Because zero belongs to it, any ideal is nonempty.
The ring R can be considered as a left module over itself, and the left ideals of R are then seen as the submodules of this module. Similarly, the right ideals are submodules of R as a right module over itself, and the two-sided ideals are submodules of R as a bimodule over itself. If R is commutative, then all three sorts of module are the same, just as all three sorts of ideal are the same.
Every ideal is a pseudo-ring.
The ideals of a ring form a semiring under addition and multiplication of ideals.

Ideal operations

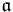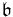The sum and product of ideals are defined as follows. For $\mathfrak{a}$ and $\mathfrak{b}$ , ideals of a ring R,

$\mathfrak{a}+\mathfrak{b}:=\{a+b \,|\, a \in \mathfrak{a} \mbox{ and } b \in \mathfrak{b}\}$

and

$\mathfrak{a} \mathfrak{b}:=\{a_1b_1+ \dots + a_nb_n \,|\, a_i \in \mathfrak{a} \mbox{ and } b_i \in \mathfrak{b}, i=1, 2, \dots, n; \mbox{ for } n=1, 2, \dots\},$

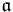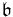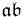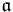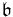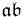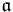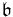i.e. the product of two ideals $\mathfrak{a}$ and $\mathfrak{b}$ is defined to be the ideal $\mathfrak{a}\mathfrak{b}$ generated by all products of the form ab with a in $\mathfrak{a}$ and b in $\mathfrak{b}$ . The product $\mathfrak{a}\mathfrak{b}$ is contained in the intersection of $\mathfrak{a}$ and $\mathfrak{b}$ .

The sum and the intersection of ideals is again an ideal; with these two operations as join and meet, the set of all ideals of a given ring forms a complete modular lattice. Also, the union of two ideals is a subset of the sum of those two ideals, because for any element a inside an ideal, we can write it as a+0, or 0+a, therefore, it is contained in the sum as well. However, the union of two ideals is not necessarily an ideal.

Important properties of these ideal operations are recorded in the Noether isomorphism theorems.

Ideals and congruence relations

There is a bijective correspondence between ideals and congruence relations (equivalence relations that respect the ring structure) on the ring:

Given an ideal I, let x ~ y if x-y ∈ I.

Conversely, given a congruence relation ~, let I = {x : x ~ 0}.

References

↑ See Hazewinkel et. al. (2004), p. 4.
↑ In fact, since R is assumed to be unital, it suffices that x + y is in I, since the second condition implies that −y is in I.
↑ Lang 2005, Section III.2

Lang, Serge (2005), Undergraduate Algebra (Third ed.), Springer-Verlag, ISBN 978-0387220253
Michiel Hazewinkel, Nadiya Gubareni, Nadezhda Mikhaĭlovna Gubareni, Vladimir V. Kirichenko. Algebras, rings and modules. Volume 1. 2004. Springer, 2004. ISBN 1-4020-2690-0